Um pouco de Topologia, Teoria do Caos & Sistemas Dinâmicos

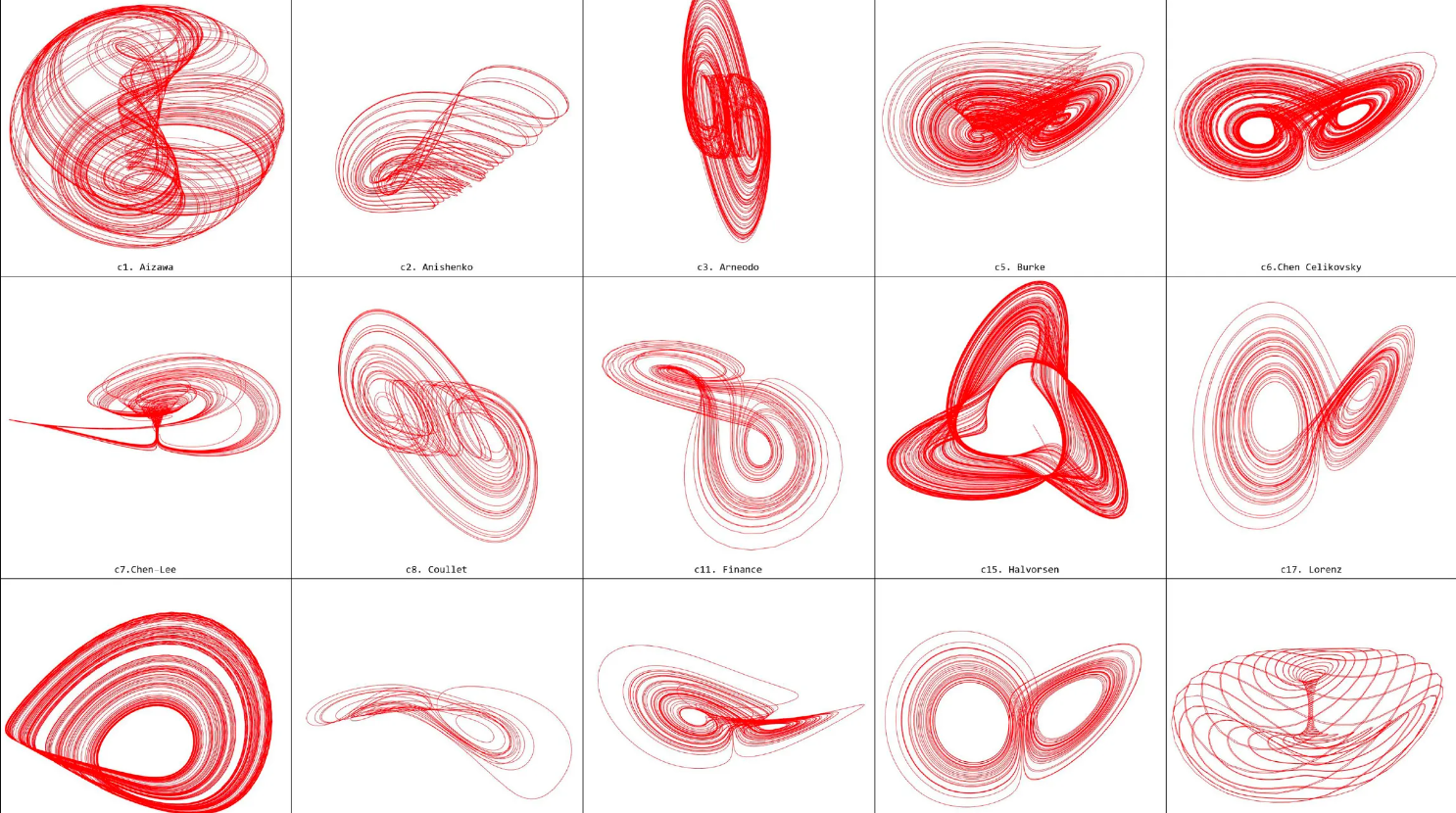
Em um universo onde temos que despender energia para manter as “coisas” em seu devido lugar, vemos como a ordem e o caos dançam em um equilíbrio delicado, a teoria dos sistemas dinâmicos serve como uma bússola, guiando nossa compreensão dos padrões subjacentes que regem o movimento e a mudança. No coração dessa teoria reside o Teorema da Recorrência de Poincaré, este, é um pilar fundamental que desafia nossa compreensão clássica do mundo. Formalmente, o Teorema da Recorrência de Poincaré é dado por:

Seja (X, M, μ, T) um sistema dinâmico medida-preservante, onde X é um espaço de estados, M é uma σ-álgebra, μ é uma medida de probabilidade e T: X → X é uma transformação medida-preservante. Se A é um conjunto mensurável com μ(A) > 0, então, quase todo ponto x em A retorna a A. Em outras palavras, o conjunto dos tempos de retorno 

Nᴬ = {n ≥ 1 : Tⁿ(x) ∈ A}

é infinito para μ-quase todo x em A.

Este teorema, embora “trivial” em sua formulação, tem implicações profundas para a maneira como entendemos os sistemas dinâmicos. Ele nos diz que, em um sistema dinâmico, quase todos os pontos eventualmente retornarão a um estado muito próximo ao seu estado inicial. Isso sugere uma espécie de ‘recorrência’ ou ‘ciclicidade’ inerente aos sistemas dinâmicos, uma ideia que continua a informar e inspirar pesquisas em física-matemática.

É importante destacar que um sistema dinâmico medida-preservante é um tipo especial de sistema dinâmico que tem uma propriedade chamada invariância de medida. Isso significa que, se você tem uma certa medida (uma maneira de atribuir um “tamanho” ou “peso” a diferentes partes do espaço de estados) que é invariante sob a evolução temporal do sistema, então o sistema é dito ser medida-preservante.

Em termos mais técnicos, um sistema dinâmico medida-preservante é geralmente definido por um espaço de estados X, uma σ-álgebra M sobre esse espaço, uma medida de probabilidade μ sobre M, e uma transformação T: X → X que preserva μ. Isso significa que para todo conjunto mensurável A em M, a medida de A é igual à medida de sua imagem sob T, ou seja,

μ(A) = μ(T(A))

Sistemas Dinâmicos

O Pêndulo de Foucault e o Teorema da Recorrência de Poincaré

O Pêndulo de Foucault, uma demonstração elegante da rotação da Terra, e o Teorema da Recorrência de Poincaré, um pilar da teoria dos sistemas dinâmicos, podem parecer mundos à parte à primeira vista, ou, para alguns, trivialmente conectados. No entanto, se fizermos uma reflexão mais profunda notamos uma conexão surpreendente e não trivial.

O pêndulo oscila em um plano que, visto de um sistema de referência fixo no espaço, permanece constante enquanto a Terra gira abaixo dele. Este movimento aparentemente simples é, na verdade, o resultado de um sistema dinâmico complexo, regido pelas leis da física – representada por equações diferenciais.

Agora, vamos considerar novamente o Teorema da Recorrência de Poincaré, ele afirma que quase todos os pontos em um sistema dinâmico (medida-preservante) retornarão a um estado muito próximo ao seu estado inicial, dado tempo suficiente. Em outras palavras, o sistema é ‘recorrente’.

Como isso se relaciona com o Pêndulo de Foucault? Bem, se considerarmos o movimento do pêndulo como um sistema dinâmico (o que é) resolver as equações (diferenciais) podem não ser uma boa ideia inicialemente… então entra o Teorema da Recorrência de Poincaré, com, não uma resposta, mas uma análise qualitativa que sugere, dado tempo suficiente, o pêndulo retornará a um estado muito próximo ao seu estado inicial. 

Isso significa que, se pudéssemos observar o Pêndulo de Foucault por tempo suficiente (e ignorar fatores como o atrito do ar e a resistência do fio), veríamos o pêndulo eventualmente retornar a um estado muito próximo ao seu estado inicial, demonstrando assim a recorrência prevista pelo teorema.

Embora na prática, fatores como o atrito do ar e a resistência do fio impeçam o Pêndulo de Foucault de demonstrar perfeitamente a recorrência prevista pelo teorema de Poincaré, esta é uma forma boa forma de começarmos a ver uma conexão teórica entre esses dois conceitos e ainda ganhar, mais uma, visão fascinante da interconexão entre diferentes áreas da física e da matemática.

Caos, Efeito Borboleta e a Dança dos Sistemas Dinâmicos

A teoria dos sistemas dinâmicos, também conhecida como Teoria do Caos, desafiou a imagem clássica do movimento determinístico. No entanto, uma reflexão profunda acerca da mecânica clássica nos fez questionar em muitos momentos se uma entidade como a sugerida por Laplace seria mesmo capaz de prever tudo – demônio de Laplace – a complexidade de problemas como “O Problema dos 3 Corpos”, “Pêndulo Duplo” entre outros. O estudo de sistemas dinâmicos mostram cada vez mais comportamentos complexos, aprofundando ainda mais o mistério – o andar do bêbado, fractais, turbulência.

Um dos conceitos mais fascinantes que emergiram dessa teoria e é uma ideia central para entender o caos, é o chamado Efeito Borboleta. Este fenômeno, nomeado pela metáfora de que o bater de asas de uma borboleta pode causar um tufão do outro lado do mundo, encapsula a ideia de que pequenas variações nas condições iniciais de um sistema dinâmico podem levar a grandes diferenças nos resultados a longo prazo. A teoria dos sistemas dinâmicos está sendo cada vez mais elaborada e sofisticada e a seguir veremos algumas das interpretações mais famosas.

Interpretação Ergódica

Esta interpretação amplamente aceita, defendida por George David Birkhoff, enfatiza a natureza estatística dos sistemas dinâmicos. As médias temporais são calculadas usando o Teorema Ergódico de Birkhoff, e o princípio da ergodicidade dita que certas propriedades, como a energia e o momento, são conservadas em média. Nessa interpretação, o sistema é descrito pela medida de probabilidade, que não é real, mas sim uma ferramenta matemática para descrever nosso conhecimento sobre o sistema antes da medida. A interpretação ergódica foca na natureza estatística da medida de probabilidade, não invocando o Teorema da Recorrência de Poincaré.

Teoria KAM (Kolmogorov-Arnold-Moser)

Desenvolvida por Kolmogorov, Arnold e Moser, esta interpretação apresenta uma alternativa quase-integrável. Os sistemas têm toros invariantes e frequências bem definidas, mesmo quando perturbados. A medida de probabilidade atua como uma “medida invariante”, guiando o movimento do sistema. Assim como na interpretação ergódica, a teoria KAM não tem necessidade do conceito do Teorema da Recorrência de Poincaré; os sistemas permanecem quase-integráveis, guiados por uma medida invariante.

Interpretação Caótica

A interpretação de Edward Lorenz postula que pequenas variações nas condições iniciais podem levar a grandes variações no comportamento dos sistemas dinâmicos. A medida de probabilidade evolui de forma sensível às condições iniciais, com todos os resultados possíveis ocorrendo em trajetórias separadas. Nessa interpretação, a medida de probabilidade permanece central.

Embora o Teorema da Recorrência de Poincaré tenha desempenhado um papel histórico, as interpretações modernas da teoria dos sistemas dinâmicos oferecem outras perspectivas. Em particular, a introdução do Efeito Borboleta trouxe uma nova dimensão à nossa compreensão dos sistemas dinâmicos, destacando a interação intrincada entre determinismo e aleatoriedade, ordem e caos.

A Teoria do Caos e o Efeito Borboleta continuam a ser áreas de pesquisa ativas, com aplicações que vão desde a previsão do tempo até a economia e além. À medida que continuamos a explorar o reino dos sistemas dinâmicos, esses conceitos servem como farois, guiando nossa jornada através deste mundo fascinante, contra-intuitivo e simplesmente caótico.

Referências

Ergodic Dynamics – From Basic Theory to Applications – Jane Hawkins, Springer
Será que Deus joga dados? A nova matemática do caos – Stewart Ian
[Studies in Nonlinearity] Steven H. Strogatz – Nonlinear Dynamics And Chaos_ With Applications To Physics, Biology, Chemistry And Engineering 1 (1994)

Créditos

Este texto foi escrito por Hassan Santos Primo, o criador de conteúdo do @nãotrivial.

Se você também quiser que sua pesquisa seu trabalho como pesquisador e/ou divulgador científico seja publicado por nós entre em contato